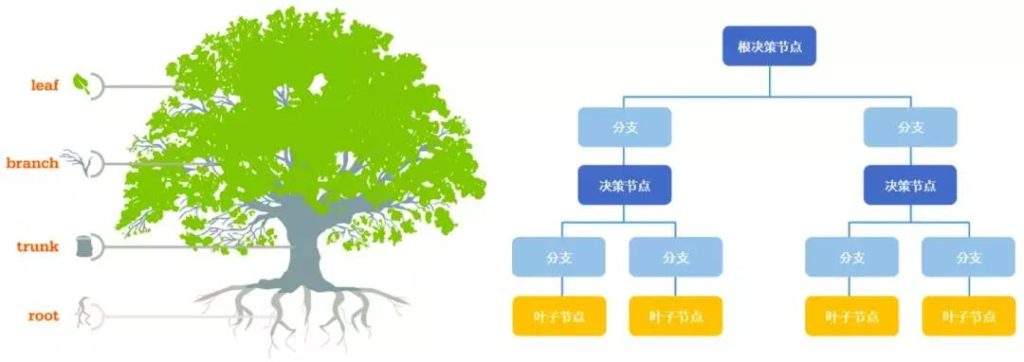
决策树和决策树学习
决策树:
A decision tree is a decision support tool that uses a tree-like model of decisions and their possible consequences, including chance event outcomes, resource costs, and utility. It is one way to display an algorithm that only contains conditional control statements.
决策树是一种决策支撑工具,它使用类似于树的决策模型及其可能的结果,包括机会事件结果、资源成本和效用。这是一种展示只包含条件控制语句算法的方法。
决策树学习:
Decision tree learning is one of the predictive modeling approaches used in statistics, data mining and machine learning. It uses a decision tree (as a predictive model) to go from observations about an item (represented in the branches) to conclusions about the item’s target value (represented in the leaves). Tree models where the target variable can take a discrete set of values are called classification trees; in these tree structures, leavesrepresent class labels and branches represent conjunctions of features that lead to those class labels. Decision trees where the target variable can take continuous values (typically real numbers) are called regression trees.
决策树学习是统计、数据挖掘和机器学习中常用的预测建模方法之一。它使用一个决策树(作为一个预测模型)从对一个项目的观察(在分支中表示)到对项目目标值的结论(在叶子中表示)。目标变量可以取一组离散值的树模型称为分类树;在这些树结构中,叶子代表类标签,而分支代表导致这些类标签的特征连接。目标变量可以取连续值(通常是实数)的决策树称为回归树。
决策树是如何工作的
决策树本质上是一种树形结构,既然是树结构,就包含节点和边。决策树是由节点(node)和有向边(directed edge)组成。而针对分类问题,决策过程,其实就是对记录的特征进行提问。最初的问题所在的地方就是根节点,在得到结论前的每一个问题都是中间节点,而得到的每一个结论都是叶子节点。
关键概念:节点
根节点:没有进边,只有出边。包含最初的,针对特征的提问。
中间节点:既有进边也有出边,进边只有一条,出边可以有多条。都是针对特征的提问。
叶子节点:只有进边,没有出边,每个叶子节点都是一个类别标签(分类问题中)。
子节点和父节点:在两个相邻的节点中,更接近根节点的是父节点,另一个是子节点。
决策树的核心问题
- 如何从数据中找到最佳节点和最佳分支?
- 如何让决策树停止生长,防止过拟合?
几乎所有的决策树有关的模型调整方法,都围绕这两个问题展开。
特征选择
如何从特征中寻找最佳特征,也就是如何从数据中找到最佳节点。对于分类树来说,衡量这个”最佳”的指标叫做不纯度(impurity。通常来说,不纯度越低,决策树对训练集的拟合越好。不纯度是基于节点来计算,树种的每个节点都会有一个不纯度,并且子节点的不纯度一定是低于父节点的,也就是说,,在同一颗决策树上,叶子节点的不纯度一定是最低的。不纯度可以通过信息增益(Information Gain)和基尼指数(Gini index)来计算。
信息增益
为了说明什么是信息增益,需要首先解释什么是熵和条件熵。
信息增益比
基尼指数
决策树的生成
ID3
C4.5
CART
Scikit-learn中的决策树
sklearn中的决策树的类都在 tree这个模块下。这个模块总共包含5个类。
| 类 | 描述 |
|---|---|
| tree.DecisionTreeClassifier | 分类树 |
| tree.DecisionTreeRegressor | 回归树 |
| tree.export_graphviz | 将生成的决策树导出为DOT格式,画图专用 |
| tree.ExtraTreeClassifier | 高随机版本的分类树 |
| tree.ExtraTreeRegressor | 高随机版本的回归树 |
sklearn建模基本流程,三步走:
- 实例化,建立模型对象
- 通过模型接口训练模型
- 通过模型接口提取需要的信息
from sklearn import tree # 导入需要的模块
clf = tree.DecisionTreeClassifier() # 实例化
clf = clf.fit(X_train, y_train) # 用训练集数据训练模型
result = clf.score(X_test, y_test) # 导入测试集,从接口中调用需要的信息DecisionTreeClassifier
sklearn.tree.DecisionTreeClassifier(criterion='gini', splitter='best', max_depth=None,
min_samples_split=2, min_samples_leaf=1,
min_weight_fraction_leaf=0.0, max_features=None,
random_state=None, max_leaf_nodes=None,
min_impurity_decrease=0.0, min_impurity_split=None,
class_weight=None, presort=False)重要参数
| 参数 | 如何影响模型 | 可能的输入有哪些 | 怎样选取参数 |
|---|---|---|---|
| criterion | 确定不纯度的方法,帮忙找出最佳节点和最佳分支,不纯度越低,决策树对训练集的拟合越好 | 1. 不填默认基尼系数 2. 填写gini使用基尼系数 3. 填写entropy使用信息增益 |
1. 通常使用基尼系数 2. 数据维度很大,噪音很大时使用基尼系数 3. 数据维度低,数据比较清晰的时候,信息熵和基尼系数没有区别 4. 当决策树拟合不够的时候,使用信息熵 5. 两个都试试,不好换另一个 |
| random_state | 设置分支中的随机模式的参数 | 默认None | 可写任一数字 |
| splitter | 也是用来控制决策树的随机选项 | 1. best(默认) 2.random |
|
| max_depth | 限制树的最大深度,超过设定深度的树枝全部剪掉 | 默认None | 这是用得最广泛的剪枝参数,在高维度低样本量时非常有效。决策树多生长一层,对样本量的需求会增加一倍,所 以限制树深度能够有效地限制过拟合。在集成算法中也非常实用。实际使用时,建议从=3开始尝试,看看拟合的效 果再决定是否增加设定深度。 |
| min_samples_split | 一个节点必须要包含至少min_samples_split个样本,这个节点才允许被分支,否则分支不会发生 | ||
| min_samples_leaf | 一个节点在分之后每个节点都必须包含至少min_samples_leaf个训练样本,否则分支不会发生,或者,分枝会朝着满足每个子节点都包含min_samples_leaf个样本的方向去发生 | ||
| max_features | max_features限制分枝时考虑的特征个数,超过限制个数的特征都会被舍弃 | ||
| min_impurity_decrease | 限制信息增益的大小,信息增益小于设定数值的分枝不会发生。这是在0.19版本中更新的 功能,在0.19版本之前时使用min_impurity_split。 | ||
| class_weight | |||
| min_weight_fraction_leaf |
重要属性和接口
- fit
- score
- Apply
- predict
- Feature_importances_
DecisionTreeRegressor
一维回归图像的绘制
import numpy as np
from sklearn.tree import DecisionTreeRegressor
import matplotlib.pyplot as plt
# Create a random dataset
rng = np.random.RandomState(30)
X = np.sort(5 * rng.rand(80,1), axis=0)
y = np.sin(X).ravel()
y[::5] += 3 * (0.5 - rng.rand(16))
# Fit regression model
reg1 = DecisionTreeRegressor(max_depth=2)
reg2 = DecisionTreeRegressor(max_depth=5)
reg1.fit(X,y)
reg2.fit(X,y)
# Predict
X_test = np.arange(0.0, 5.0, 0.01)[:, np.newaxis]
y_1 = reg1.predict(X_test)
y_2 = reg2.predict(X_test)
# Plot the results
plt.figure()
plt.scatter(X, y ,s=20, edgecolors='black', c='darkorange', label='data')
plt.plot(X_test, y_1, color='cornflowerblue', label='max_depth=2', linewidth=2)
plt.plot(X_test, y_2, color='yellowgreen', label='max_depth=5', linewidth=2)
plt.xlabel('data')
plt.ylabel('target')
plt.title('Decision Tree Regressor')
plt.legend()
plt.show()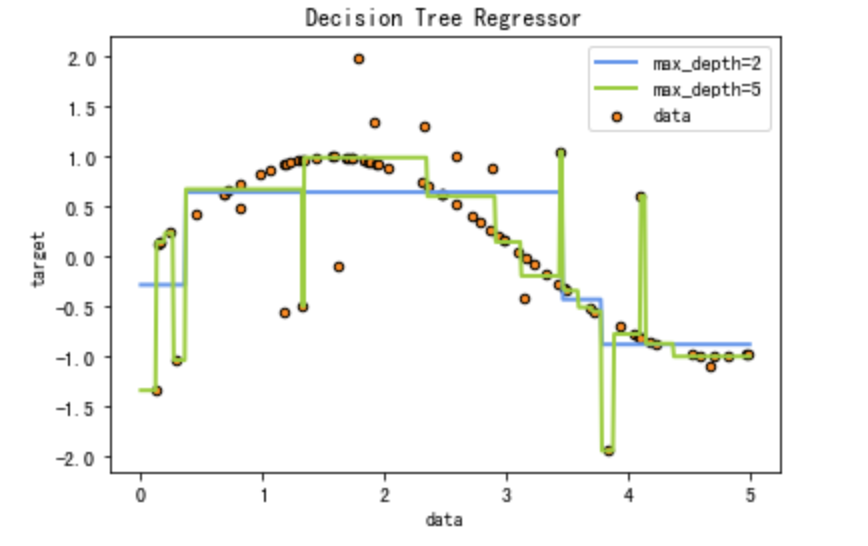
决策树的优缺点
- 优点
- 易于理解和解释,因为树木可以画出来被看见。
- 需要很少的数据准备。其他很多算法通常都需要数据规范化,需要创建虚拟变量并删除空值等。但请注意,sklearn中的决策树模块不支持对缺失值的处理。
- 使用树的成本(比如说,在预测数据的时候)是用于训练树的数据点的数量的对数,相比于其他算法,这是一个很低的成本。
- 能够同时处理数字和分类数据,既可以做回归又可以做分类。其他技术通常专门用于分析仅具有一种变量类型的数据集。
- 能够处理多输出问题,即含有多个标签的问题,注意与一个标签中含有多种标签分类的问题区别开。
- 是一个白盒模型,结果很容易能够被解释。如果在模型中可以观察到给定的情况,则可以通过布尔逻辑轻松 解释条件。相反,在黑盒模型中(例如,在人工神经网络中),结果可能更难以解释。
- 可以使用统计测试验证模型,这让我们可以考虑模型的可靠性。
- 即使其假设在某种程度上违反了生成数据的真实模型,也能够表现良好。
- 缺点
- 决策树学习者可能创建过于复杂的树,这些树不能很好地推广数据。这称为过度拟合。修剪,设置叶节点所 需的最小样本数或设置树的最大深度等机制是避免此问题所必需的,而这些参数的整合和调整对初学者来说 会比较晦涩。
- 决策树可能不稳定,数据中微小的变化可能导致生成完全不同的树,这个问题需要通过集成算法来解决。
- 决策树的学习是基于贪婪算法,它靠优化局部最优(每个节点的最优)来试图达到整体的最优,但这种做法 不能保证返回全局最优决策树。这个问题也可以由集成算法来解决,在随机森林中,特征和样本会在分枝过 程中被随机采样。
- 有些概念很难学习,因为决策树不容易表达他们,例如XOR,奇偶校验或多路复用器问题。
- 如果标签中的某些类占主导地位,决策树学习者会创建偏向主导类的树。因此,建议在拟合决策树之前平衡数据集。
总结
决策树(Decision Tree)是一种非参数的有监督学习方法,它能够从一系列有特征和标签的数据中总结出决策规则,并用树状图的结构来呈现这些规则,以解决分类和回归问题。决策树算法容易理解,适用各种数据,在解决各 种问题时都有良好表现,尤其是以树模型为核心的各种集成算法,在各个行业和领域都有广泛的应用。
参考
[1] weikipedia.Decision tree: https://en.wikipedia.org/wiki/Decision_tree
[2] weikipedia.Decision tree learning: https://en.wikipedia.org/wiki/Decision_tree_learning
[3] scikit-learn官网. Decision Trees: https://scikit-learn.org/stable/modules/tree.html
[4] 李航. 统计学习方法. 第五章 决策树



